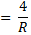Segunda parte do curso de Eletromagnetismo do Prof. Dr. Rene A. Moreno Alfaro. [clique aqui]
Neste número:
Campos elétricos e magnéticos dentro da matéria
Campo elétrico
Condições de contorno na junção de dois dielétricos
Exemplos
Dielétrico semi-infinito
Dois dielétricos semi-infinitos
Uma esfera de raio r uniformemente polarizada, P
Uma cavidade esférica num meio dielétrico uniformemente polarizado
Uma esfera dielétrica de raio R imersa numa região de campo uniforme E 0
Moléculas Polares – Fórmula de Langevin- Debye
Campo magnético
Correntes de Ampère e “pólos magnéticos”
Susceptibilidade Magnética, Permeabilidade Magnética, Histerese
Materiais Ferromagnéticos
Condições de contorno para B e H.
Ondas Eletromagnéticas em meios materiais
Ondas planas monocromáticas num meio dielétrico sem condutividade
Ondas planas monocromáticas num meio com condutividade
Reflexão total
Boa leitura
Exercicios resolvidos de fisica
Alguns exercícios de Fisica, Calculo e filosofia de sala de aula.
terça-feira, outubro 22, 2013
domingo, agosto 11, 2013
Tópicos de Eletromagnetismo (Primeira Parte) por Rene A. Moreno Alfaro
O professor Rene A. Moreno Alfaro desenvolveu anotações sobre eletromagnetismo em forma de uma apostila. São notas para alunos de faculdade de ciencias exatas exigindo conceitos de calculo.
Fico feliz em divulgar aqui este material feito com muito cuidado que o Prof. Rene, meu professor e amigo me confiou a divulgar.
Creio que será de extrema utilidade para estudantes em geral, seja de Fisica ou de Engenharia.
Introdução
Estas notas foram escritas com a intenção de dar um empurrão inicial ao estudo da
teoria eletromagnética, são notas que resumem o que foi exposto a estudantes de
graduação em engenharia e em física durante os anos que tive a oportunidade de
lecionar. São notas introdutórias que, evidentemente, não substituem os livros clássicos
sobre o tema que são de amplo uso em nosso meio acadêmico. Esses livros devem ser
consultados pelo estudante para incorporar e expandir seu conhecimento do
eletromagnetismo. É do esforço próprio que depende o aprendizado de qualquer
disciplina.
Este material contém:
Tabela de Identidades e Fórmulas úteis do Cálculo Vetorial
Fórmulas da álgebra vetorial
Eletromagnetismo para estudantes da licenciatura em Física
Eletrostática
Representação gráfica do campo elétrico – linhas de força
Cargas distribuídas
Tipos de materiais – Isolantes e Condutores
Dispositivos elementares
Dispositivos de indução
Propriedades dos campos eletrostáticos – Potencial e Energia Potencial
Integral de linha e o conceito de potencial
Cálculo do campo elétrico e do potencial de sistemas simples de cargas pontuais
Campo elétrico e potencial de um dipolo
Expansão em multipolos
Exemplo: Cálculo do potencial de um anel de carga.
Conceito de divergência de um campo vetorial e Forma diferencial da Lei de Gauss
Operador Nabla ou Operador Del
Equação de Laplace
Conceito de rotacional de um campo vetorial
Exemplos de problemas de eletrostática
Energia armazenada num capacitor
Energia Associada ao Campo Elétrico
Correntes Elétricas
Lei de Ohm
Campos magnetostáticos
Força sobre condutores pelo campo magnético
Lei de Biot e Savart
Lei circuital de Ampere
Potencial Vetor
Campos magnéticos variáveis na posição e no tempo. Condutores em movimento
na presença de um campo magnético
Lei de Indução de Faraday
Conceito de Indutância
Equações de Maxwell
Material Completo: Topicos de Eletromagnetismo (Primeira Parte) por Rene A. Moreno Alfaro
Fico feliz em divulgar aqui este material feito com muito cuidado que o Prof. Rene, meu professor e amigo me confiou a divulgar.
Creio que será de extrema utilidade para estudantes em geral, seja de Fisica ou de Engenharia.
Introdução
Estas notas foram escritas com a intenção de dar um empurrão inicial ao estudo da
teoria eletromagnética, são notas que resumem o que foi exposto a estudantes de
graduação em engenharia e em física durante os anos que tive a oportunidade de
lecionar. São notas introdutórias que, evidentemente, não substituem os livros clássicos
sobre o tema que são de amplo uso em nosso meio acadêmico. Esses livros devem ser
consultados pelo estudante para incorporar e expandir seu conhecimento do
eletromagnetismo. É do esforço próprio que depende o aprendizado de qualquer
disciplina.
Este material contém:
Tabela de Identidades e Fórmulas úteis do Cálculo Vetorial
Fórmulas da álgebra vetorial
Eletromagnetismo para estudantes da licenciatura em Física
Eletrostática
Representação gráfica do campo elétrico – linhas de força
Cargas distribuídas
Tipos de materiais – Isolantes e Condutores
Dispositivos elementares
Dispositivos de indução
Propriedades dos campos eletrostáticos – Potencial e Energia Potencial
Integral de linha e o conceito de potencial
Cálculo do campo elétrico e do potencial de sistemas simples de cargas pontuais
Campo elétrico e potencial de um dipolo
Expansão em multipolos
Exemplo: Cálculo do potencial de um anel de carga.
Conceito de divergência de um campo vetorial e Forma diferencial da Lei de Gauss
Operador Nabla ou Operador Del
Equação de Laplace
Conceito de rotacional de um campo vetorial
Exemplos de problemas de eletrostática
Energia armazenada num capacitor
Energia Associada ao Campo Elétrico
Correntes Elétricas
Lei de Ohm
Campos magnetostáticos
Força sobre condutores pelo campo magnético
Lei de Biot e Savart
Lei circuital de Ampere
Potencial Vetor
Campos magnéticos variáveis na posição e no tempo. Condutores em movimento
na presença de um campo magnético
Lei de Indução de Faraday
Conceito de Indutância
Equações de Maxwell
Material Completo: Topicos de Eletromagnetismo (Primeira Parte) por Rene A. Moreno Alfaro
terça-feira, fevereiro 01, 2011
Porque o 111 aparece em todas as datas deste ano?
Fui interpelado pelo meu fiel mecânico de bicicletas com essa duvida. “Porque qualquer ano somado a idade, neste ano dá 111 ou 11?”
Fiz o calculo de cabeça e vi que minha idade em 2011 será 40 anos, somado a 71, realmente dá 111, fiz outros cálculos e comprovei o método!
Fiquei de pensar sobre o assunto.
Mais algumas pessoas fizeram a mesma pergunta, alguém disse que inclusive seria um sinal previsto por Nostradamus e tudo mais.
Depois conversei com minha esposa que é matemática e ela notou que isso acontece sempre, ano passado a soma da minha idade (39) mais o ano (71) daria 110, isso para qualquer data.
Isso é claro que é assim e sempre será.
Na verdade você está cometendo um erro quando calcula assim, mas vou tentar explicar:
Como eu sei que em 2011 terei 40 anos? Porque eu faço a conta 2011-1971 = 40, certo?
Então o 2011 já está na minha conta.
Quando eu somar 1971, terei 2011, certo ?
Então 2011 – 1971 = 40, mas 40 + 1971 = 2011.
O que é feito é fazer a conta ao contrário.
Isso para qualquer data, obviamente...
2011 – 1950 = 61, e 61 + 1950 = 2011 !
2011 – 1500 = 511 e 511 + 1500 = 2011 !
Algebricamente seria:
Anoatual – Anopassado = idade à idade + Anopassado = Anoatual
Agora porque o 111 e não 2011 ?
Porque agente faz a conta e esquece o século. Quando eu fiz: 40 + 71, o resultado 111 significa 11 anos a partir do 100 (cem) ou no próximo século.
Você pode ver isso com datas dentro do próprio século, como minha filha que nasceu em 2005 e em 2011 fará 6 anos. 11 – 5 = 6 à 6 + 5 = 11, ou usando o século 2011-2005 = 6à2006+5=2011 !
Entendeu?
Lembre-se que x + y – x = y, sempre ...
segunda-feira, maio 31, 2010
Lançamento vertical
Ai vai a resolução de dois problemas que recebi do Alexandre por email...
1. Dois corpos são lançados verticalmente para cima do mesmo ponto com vel. iniciais de 30 m/s. O segundo corpo é lançado 3 s depois do primeiro (g = 10 m/s2).
a)o instante e a posição do encontro?
b) as velocidades dos corpos no instante do encontro.
Meu caro Alexandre, em qualquer problema de mecânica, tente equacionar o problema em termos de espaço por tempo, a chamada equação horária do movimento. Isso ajuda muito.
Para o primeiro corpo, sua velocidade inicial é 30 m/s e ele sofre a ação da gravidade. Então sua equação é:
s = s0 + v0.t - 1/2g.t2, vamos considerar s0 = 0, o que significa que nossa referência é o ponto de lançamento.
s = 30.t - 5t2
O segundo corpo possui uma equação praticamente idêntica, exceto que seu t é sempre t+3, já que foi lançado 3 segundos depois.
Então
s = s0 + v0(t+3) - 5.(t+3)2, novamente considerando s0 = 0, temos:
s = 30.t + 3.(t + 3) - 5(t2 + 6.t + 9) (lembre-se (a+b)2 = a2 + 2ab + b2 ),
s = 30.t + 3.t - 5.t2 - 30.t -45 + 90
s = 30.t - 30.t + 3.t - 5.t2 - 45
s = -5.t2 - 45
Igualando as duas equações, temos:
-5t2 + 30.t = -5t2 - 45
30 t = 45 ; t = 1,5 s !
Neste ponto a velocidade será: v = v0 - at.
v = 30 - 10.(1,5)
v = 15 m/s
(para chegar nessa expressão tem um segredinho. O tempo t=3s não foi escolhido ao acaso, vc pode calcular que neste ponto o objeto está no ponto mais alto e com velocidade zero, então enquanto um acelera para baixo, o outro desacelera para cima.
Substituindo este t = 1,5 s, na expressão horária, temos:
s = 45 - 5(1,5)2 = 33,75 m
2. Dois corpos estão na mesma vertical, à distancia de 30 m um do outro. Abandona-se o de cima e, após, 2 s, o outro. Após, quanto tempo e em que ponto se dará o encontro dos dois? (g = 10 m/s2).
A equação horária do primeiro é
s = s0 + v0t + 1/2 . g . t2 mas vo = 0 e s0 = 0, então,
s = 5t2.
Quando o segundo corpo for lançado, o primeiro terá percorrido a distância de:
s = 5(2)2 = 20 m
E sua velocidade será:
v = a.t = 10 (2) = 20m/s.
Então podemos reescrever a equação horária do primeiro no momento do lançamento do segundo, assim:
s = s0 + v0t + 1/2 g t2
s = 20 + 20.t + 5 t2
E a equação horária do segundo objeto fica:
s = 30 + 1/2 g .t2 = 30 + 5.t2
Igualando as duas distâncias,
20 + 5.t2 = 20 + 20.t + 5t2
20.t = 10
t=0,5 s
Lembre-se. Isto ocorrerá após os dois segundos em que o primeiro foi lançado. Então o tempo decorrido será de 2,5 s.
s = 30 + 5t2 = 30 + 5.(0.5)2
s = 31,25 m
Fiz com um pouco de pressa, posso ter errado alguma coisa, mas conferi varias vezes, se tiver alguma duvida posta ai.
E espero ter colocado ainda a tempo de ser útil...
Busquei ao SENHOR, e ele me respondeu; livrou-me de todos os meus temores.
Salmos 34:4
1. Dois corpos são lançados verticalmente para cima do mesmo ponto com vel. iniciais de 30 m/s. O segundo corpo é lançado 3 s depois do primeiro (g = 10 m/s2).
a)o instante e a posição do encontro?
b) as velocidades dos corpos no instante do encontro.
Meu caro Alexandre, em qualquer problema de mecânica, tente equacionar o problema em termos de espaço por tempo, a chamada equação horária do movimento. Isso ajuda muito.
Para o primeiro corpo, sua velocidade inicial é 30 m/s e ele sofre a ação da gravidade. Então sua equação é:
s = s0 + v0.t - 1/2g.t2, vamos considerar s0 = 0, o que significa que nossa referência é o ponto de lançamento.
s = 30.t - 5t2
O segundo corpo possui uma equação praticamente idêntica, exceto que seu t é sempre t+3, já que foi lançado 3 segundos depois.
Então
s = s0 + v0(t+3) - 5.(t+3)2, novamente considerando s0 = 0, temos:
s = 30.t + 3.(t + 3) - 5(t2 + 6.t + 9) (lembre-se (a+b)2 = a2 + 2ab + b2 ),
s = 30.t + 3.t - 5.t2 - 30.t -45 + 90
s = 30.t - 30.t + 3.t - 5.t2 - 45
s = -5.t2 - 45
Igualando as duas equações, temos:
-5t2 + 30.t = -5t2 - 45
30 t = 45 ; t = 1,5 s !
Neste ponto a velocidade será: v = v0 - at.
v = 30 - 10.(1,5)
v = 15 m/s
(para chegar nessa expressão tem um segredinho. O tempo t=3s não foi escolhido ao acaso, vc pode calcular que neste ponto o objeto está no ponto mais alto e com velocidade zero, então enquanto um acelera para baixo, o outro desacelera para cima.
Substituindo este t = 1,5 s, na expressão horária, temos:
s = 45 - 5(1,5)2 = 33,75 m
2. Dois corpos estão na mesma vertical, à distancia de 30 m um do outro. Abandona-se o de cima e, após, 2 s, o outro. Após, quanto tempo e em que ponto se dará o encontro dos dois? (g = 10 m/s2).
A equação horária do primeiro é
s = s0 + v0t + 1/2 . g . t2 mas vo = 0 e s0 = 0, então,
s = 5t2.
Quando o segundo corpo for lançado, o primeiro terá percorrido a distância de:
s = 5(2)2 = 20 m
E sua velocidade será:
v = a.t = 10 (2) = 20m/s.
Então podemos reescrever a equação horária do primeiro no momento do lançamento do segundo, assim:
s = s0 + v0t + 1/2 g t2
s = 20 + 20.t + 5 t2
E a equação horária do segundo objeto fica:
s = 30 + 1/2 g .t2 = 30 + 5.t2
Igualando as duas distâncias,
20 + 5.t2 = 20 + 20.t + 5t2
20.t = 10
t=0,5 s
Lembre-se. Isto ocorrerá após os dois segundos em que o primeiro foi lançado. Então o tempo decorrido será de 2,5 s.
s = 30 + 5t2 = 30 + 5.(0.5)2
s = 31,25 m
Fiz com um pouco de pressa, posso ter errado alguma coisa, mas conferi varias vezes, se tiver alguma duvida posta ai.
E espero ter colocado ainda a tempo de ser útil...
Busquei ao SENHOR, e ele me respondeu; livrou-me de todos os meus temores.
Salmos 34:4
segunda-feira, março 29, 2010
Circuitos e Lei de Ohm
Segundo o Google, o assunto mais procurado em meu humilde blog é “Lei de Ohm” e como este assunto é um dos meus preferidos, vou postar a maior quantidade de exercícios que puder a respeito deste.
No exercício abaixo, vou partir do caso mais geral e ir particularizando. O primeiro caso, a menos que você esteja estudando para um curso superior de ciências exatas, você não vai encontrá-lo sob esta forma, mas ai vai...
1.
Encontre o circuito equivalente e a corrente no circuito abaixo, supondo V a ddp (diferença de potencial) entre os terminais A e B.
A manha neste tipo de exercício é encontrar o circuito equivalente. Treine para encontrar um circuito em termos de paralelos e série que seus problemas serão resolvidos.
Veja que na verdade, todos os resistores estão ligados em A e B apenas. Não consegue ver? Tá, vou pintar tudo que está ligado diretamente (curto-circuitado) ao ponto A em vermelho e tudo o que está no ponto B em verde!
Melhor assim?
Então, temos um típico circuito em paralelo de 4 resistores:
Bom, se são resistores em paralelo,
Fácil agora, meu filho?
Pela lei de ohm, V = R.I e se queremos encontrar a corrente I que circula neste circuito,
Eu sei que é obvio, mas não custa nada:
E daí:
(I)
Ou ainda,
Que é a forma geral de 4 resistores ligados em paralelo.
Bien, abaixo uma variação deste exercício:
Caso 2: Em geral este exercício vai ser encontrado assim:
Quatro resistores iguais são ligados como a figura abaixo:
Encontre o valor do resistor equivalente e a corrente elétrica no circuito.

Já tá colorido para o caso de você ter pulado a primeira parte. Então, os quatro resistores estão na verdade estão em paralelissimo, ficando assim:
Da expressão (I) quando R=R1=R2=R3=R4, temos:
E Req
Muito bem, mas se você é um ser normal que não vai cursar engenharia, física, matemática e outras loucuras, o exercício abaixo é pra você, mas leia os anteriores que uma coisa depende da outra:
Suponha quatro resistores de 100 ohms ligados como a figura abaixo. Encontre o valor da resistência equivalente entre A e B.
Então, de novo, o pulo do gato é ver que este circuito é um circuito paralelo puro e simples, vendo isso fica muito fácil:
Existem maneiras de incluir um resistor ai e deixar a coisa ficar bem mais complicada, mas isso fica para outro POST.
Não percam as grandes aventuras da Lei de Ohm na Internet...
Porque para mim tenho por certo que as aflições deste tempo presente não são para comparar com a glória que em nós há de ser revelada.
Romanos 8:18
No exercício abaixo, vou partir do caso mais geral e ir particularizando. O primeiro caso, a menos que você esteja estudando para um curso superior de ciências exatas, você não vai encontrá-lo sob esta forma, mas ai vai...
1.
Encontre o circuito equivalente e a corrente no circuito abaixo, supondo V a ddp (diferença de potencial) entre os terminais A e B.
A manha neste tipo de exercício é encontrar o circuito equivalente. Treine para encontrar um circuito em termos de paralelos e série que seus problemas serão resolvidos.
Veja que na verdade, todos os resistores estão ligados em A e B apenas. Não consegue ver? Tá, vou pintar tudo que está ligado diretamente (curto-circuitado) ao ponto A em vermelho e tudo o que está no ponto B em verde!
Melhor assim?
Então, temos um típico circuito em paralelo de 4 resistores:
Bom, se são resistores em paralelo,
Fácil agora, meu filho?
Pela lei de ohm, V = R.I e se queremos encontrar a corrente I que circula neste circuito,
Eu sei que é obvio, mas não custa nada:
E daí:
(I)
Ou ainda,
Que é a forma geral de 4 resistores ligados em paralelo.
Bien, abaixo uma variação deste exercício:
Caso 2: Em geral este exercício vai ser encontrado assim:
Quatro resistores iguais são ligados como a figura abaixo:
Encontre o valor do resistor equivalente e a corrente elétrica no circuito.

Já tá colorido para o caso de você ter pulado a primeira parte. Então, os quatro resistores estão na verdade estão em paralelissimo, ficando assim:
Da expressão (I) quando R=R1=R2=R3=R4, temos:
E Req
Muito bem, mas se você é um ser normal que não vai cursar engenharia, física, matemática e outras loucuras, o exercício abaixo é pra você, mas leia os anteriores que uma coisa depende da outra:
Suponha quatro resistores de 100 ohms ligados como a figura abaixo. Encontre o valor da resistência equivalente entre A e B.
Então, de novo, o pulo do gato é ver que este circuito é um circuito paralelo puro e simples, vendo isso fica muito fácil:
Existem maneiras de incluir um resistor ai e deixar a coisa ficar bem mais complicada, mas isso fica para outro POST.
Não percam as grandes aventuras da Lei de Ohm na Internet...
Porque para mim tenho por certo que as aflições deste tempo presente não são para comparar com a glória que em nós há de ser revelada.
Romanos 8:18
sexta-feira, outubro 16, 2009
Os professores que dizem NO !
Continuando a série de professores que tive, gostaria de dedicar este POST ao professor Teófilo, o único professor que conseguiu me reprovar e por isso tenho muito carinho por ele.
Ele me reprovou e tenho carinho por ele? Pois é. Vamos ao início.
Eu nunca fui de estudar. Tenho uma capacidade de raciocinar relativamente boa e uma memória muito desorganizada, mas estranhamente eficiente. Em dia de prova eu simplesmente me lembrava da matéria e nunca tive problemas sérios de notas em função disso. Tive fama injusta de CDF, por não sair muito de casa, mas eu quase não estudava – Quase não, não estudava mesmo. Passava minhas tarde jogando vídeo-game ou assistindo Sessão da Tarde – Sei diálogos do “Pássaro Azul” de cor. Eu era ou segundo ou terceiro aluno da classe e pra mim tava bom demais, dado o custo.
Pra prestar vestibular resolvi estudar, mas também não foi tanto assim. Tanto que fui, relativamente bem em matemática e muito bem em química e muito ruim em Física. Na média, fui terceiro colocado no vestibular da minha turma. Ironicamente no curso de Física.
Depois dos trotes, a primeira aula que assisti pra valer, foi de um professor magro, com um pesado sotaque castelhano (ou um fraco sotaque português, como maldosamente os colegas o classificavam) e com uma lousa absolutamente maravilhosa. Esse era o professor Colombiano Teófilo.
Dizer que ele tinha um sotaque espanhol é pouco. Ele praticamente falava em Espanhol mesmo. Isso não chegava a ser problema, porque o espanhol é bem entendível, não dá pra se aventurar a falar, mas entender é tranqüilo.
O pior problema era mesmo a matéria. Geometria Analítica me parecia simples. Parecia, parecia. Aquela mania de não estudar estava com os dias contados. Não me lembro muito bem das notas, mas não fui bem. Acabei ficando de recuperação e passei.
Por outras razões eu já estava aprendendo a estudar e no segundo ano, o mesmo professor Teófilo deu a disciplina Calculo Avançado. Aí sim as coisas se complicaram.
A disciplina era puxadíssima, a classe era imensa (perto de 90 alunos em uma classe) e eu aprendendo a estudar. Ficava na biblioteca estudando, estudando e estudando. Fazia listas de exercícios e pegava provas dos anos passados pra tentar resolver. E nota que é bom nada.
Teófilo era um professor, até certo ponto ríspido, de respostas monossilábicas, por outro lado uma pessoa inteligentíssima e um professor que tinha o ensino como objetivo principal. Me lembro de ir um dia em sua sala tirar dúvidas e ele estava atendendo um professor, conversando sobre assuntos departamentais. Ao me ver, ele se dirigiu ao professor – Perdona-me, tengo que atender un aluno !
Ele era assim, ensino em primeiro lugar. O Contrário também valia. Pouquíssimas vezes ele abria espaço para conversas sobre seja lá o que fosse, que não fosse o assunto da aula.
Uma vez aconteceu uma cena surreal. Ele estava dando aula e na rua, passou um palhaço (palhaço mesmo, estes de circo) divulgando algum evento cultural na cidade. O palhaço tocava um tambor e uma buzina. Entrou na sala em que estávamos em aula. O prof. Teófilo nem parou para ver o que acontecia, seguia sua lousa maravilhosa. O palhaço se dirigiu a ele então – PROFESSOR, POSSO DAR UM RECADO PARA A TURMA ?
NO – Respondeu ele, sem sequer se virar.
O palhaço agradeceu e se foi !
Ele era assim. Sempre fumando muito, sempre lendo ou escrevendo e tomando muito café. Me lembro de uma prova que foi das 8:00 hs da manhã até as 14:00 hs ! Initerruptamente. “Enquanto agüentarem, estoy aqui !”
Foi, foi e foi e acabei reprovando em Calculo Avançado. Percebi que o Prof. Teofilo tinha me desafiado intelectualmente e eu tinha perdido. Compreendi que a culpa não era dele (ao contrário do que os colegas achavam) e que eu tinha de fazer a disciplina de novo e passar.
Fiz de novo. E fui relativamente bem, lá com meu cinquinho básico, mas bem. Na última prova dei uma bobeada e fiquei com média ligeiramente abaixo da média, com muitos alunos.
Estes alunos e eu, então fizemos um pedido para que ele nos desse outra chance. Ele aceitou. Pediu para que fossemos a sala dele em tal dia e tal hora.
Ficamos todos enfileirados e ele numa sala. As vezes ele abria e um aluno desolado saia. Ele então chamava o próximo.
Pouquíssimos foram aprovados naquele dia.
Quando eu entrei na sala, ainda me lembro bem, o ar dava pra cortar da fumaça de cigarro. Pensei então que ele me daria um exercício daqueles para resolver. Ele então me falou - “Desenhe una funcion en la lousa !”. Desenhei então uma minhoca.
Calcule ahora la integral desta funcion.
E agora ? Fiquei pensando, pensando e ele “Se no sabes um conceito bassico destes no puede passar !”
Então fiz alguns retângulos e disse pra ele – “A integral desta função é a soma da área destes retângulos !”
MUY BIEN ! ESTAS APROVADO !
Em retrospecto penso que o professor Teofilo realmente desafiou a todos os 90 alunos daquela turma para um jogo de xadrez que durou cerca de 2 anos. Alguns não viram assim, mas quem viu e aceitou o desafio jogou com um grande jogador, uma pessoa com inteligência e cultura muito acima de nossa.
Ele ganhou uma partida, mas eu ganhei a outra e ele ficou feliz por isso.
Anos depois recebi a notícia do falecimento do professor Teófilo. O excesso de café e cigarro devem ter feito mal para seu coração.
Hoje sinto falta de pessoas que realmente me desafiem intelectualmente- Tenho um profesor me desafiando atualmente, mas escreverei sobre isso em outro POST. Parece que a mediocridade impera. Muitos dos meus alunos também não vêem desafios intelectuais com bons olhos e acham que ser reprovado é culpa do professor.
Ainda bem que eu tive um professor Teófilo, um professor que dizia NO na minha vida !
Ele me reprovou e tenho carinho por ele? Pois é. Vamos ao início.
Eu nunca fui de estudar. Tenho uma capacidade de raciocinar relativamente boa e uma memória muito desorganizada, mas estranhamente eficiente. Em dia de prova eu simplesmente me lembrava da matéria e nunca tive problemas sérios de notas em função disso. Tive fama injusta de CDF, por não sair muito de casa, mas eu quase não estudava – Quase não, não estudava mesmo. Passava minhas tarde jogando vídeo-game ou assistindo Sessão da Tarde – Sei diálogos do “Pássaro Azul” de cor. Eu era ou segundo ou terceiro aluno da classe e pra mim tava bom demais, dado o custo.
Pra prestar vestibular resolvi estudar, mas também não foi tanto assim. Tanto que fui, relativamente bem em matemática e muito bem em química e muito ruim em Física. Na média, fui terceiro colocado no vestibular da minha turma. Ironicamente no curso de Física.
Depois dos trotes, a primeira aula que assisti pra valer, foi de um professor magro, com um pesado sotaque castelhano (ou um fraco sotaque português, como maldosamente os colegas o classificavam) e com uma lousa absolutamente maravilhosa. Esse era o professor Colombiano Teófilo.
Dizer que ele tinha um sotaque espanhol é pouco. Ele praticamente falava em Espanhol mesmo. Isso não chegava a ser problema, porque o espanhol é bem entendível, não dá pra se aventurar a falar, mas entender é tranqüilo.
O pior problema era mesmo a matéria. Geometria Analítica me parecia simples. Parecia, parecia. Aquela mania de não estudar estava com os dias contados. Não me lembro muito bem das notas, mas não fui bem. Acabei ficando de recuperação e passei.
Por outras razões eu já estava aprendendo a estudar e no segundo ano, o mesmo professor Teófilo deu a disciplina Calculo Avançado. Aí sim as coisas se complicaram.
A disciplina era puxadíssima, a classe era imensa (perto de 90 alunos em uma classe) e eu aprendendo a estudar. Ficava na biblioteca estudando, estudando e estudando. Fazia listas de exercícios e pegava provas dos anos passados pra tentar resolver. E nota que é bom nada.
Teófilo era um professor, até certo ponto ríspido, de respostas monossilábicas, por outro lado uma pessoa inteligentíssima e um professor que tinha o ensino como objetivo principal. Me lembro de ir um dia em sua sala tirar dúvidas e ele estava atendendo um professor, conversando sobre assuntos departamentais. Ao me ver, ele se dirigiu ao professor – Perdona-me, tengo que atender un aluno !
Ele era assim, ensino em primeiro lugar. O Contrário também valia. Pouquíssimas vezes ele abria espaço para conversas sobre seja lá o que fosse, que não fosse o assunto da aula.
Uma vez aconteceu uma cena surreal. Ele estava dando aula e na rua, passou um palhaço (palhaço mesmo, estes de circo) divulgando algum evento cultural na cidade. O palhaço tocava um tambor e uma buzina. Entrou na sala em que estávamos em aula. O prof. Teófilo nem parou para ver o que acontecia, seguia sua lousa maravilhosa. O palhaço se dirigiu a ele então – PROFESSOR, POSSO DAR UM RECADO PARA A TURMA ?
NO – Respondeu ele, sem sequer se virar.
O palhaço agradeceu e se foi !
Ele era assim. Sempre fumando muito, sempre lendo ou escrevendo e tomando muito café. Me lembro de uma prova que foi das 8:00 hs da manhã até as 14:00 hs ! Initerruptamente. “Enquanto agüentarem, estoy aqui !”
Foi, foi e foi e acabei reprovando em Calculo Avançado. Percebi que o Prof. Teofilo tinha me desafiado intelectualmente e eu tinha perdido. Compreendi que a culpa não era dele (ao contrário do que os colegas achavam) e que eu tinha de fazer a disciplina de novo e passar.
Fiz de novo. E fui relativamente bem, lá com meu cinquinho básico, mas bem. Na última prova dei uma bobeada e fiquei com média ligeiramente abaixo da média, com muitos alunos.
Estes alunos e eu, então fizemos um pedido para que ele nos desse outra chance. Ele aceitou. Pediu para que fossemos a sala dele em tal dia e tal hora.
Ficamos todos enfileirados e ele numa sala. As vezes ele abria e um aluno desolado saia. Ele então chamava o próximo.
Pouquíssimos foram aprovados naquele dia.
Quando eu entrei na sala, ainda me lembro bem, o ar dava pra cortar da fumaça de cigarro. Pensei então que ele me daria um exercício daqueles para resolver. Ele então me falou - “Desenhe una funcion en la lousa !”. Desenhei então uma minhoca.
Calcule ahora la integral desta funcion.
E agora ? Fiquei pensando, pensando e ele “Se no sabes um conceito bassico destes no puede passar !”
Então fiz alguns retângulos e disse pra ele – “A integral desta função é a soma da área destes retângulos !”
MUY BIEN ! ESTAS APROVADO !
Em retrospecto penso que o professor Teofilo realmente desafiou a todos os 90 alunos daquela turma para um jogo de xadrez que durou cerca de 2 anos. Alguns não viram assim, mas quem viu e aceitou o desafio jogou com um grande jogador, uma pessoa com inteligência e cultura muito acima de nossa.
Ele ganhou uma partida, mas eu ganhei a outra e ele ficou feliz por isso.
Anos depois recebi a notícia do falecimento do professor Teófilo. O excesso de café e cigarro devem ter feito mal para seu coração.
Hoje sinto falta de pessoas que realmente me desafiem intelectualmente- Tenho um profesor me desafiando atualmente, mas escreverei sobre isso em outro POST. Parece que a mediocridade impera. Muitos dos meus alunos também não vêem desafios intelectuais com bons olhos e acham que ser reprovado é culpa do professor.
Ainda bem que eu tive um professor Teófilo, um professor que dizia NO na minha vida !
sexta-feira, setembro 11, 2009
Pois é, 3 anos !
Foi num dia 11 de Setembro de 2006 que resolvi criar este blog. A ideia não era fazer algo que fosse propositalmente visto, mas sim, mostrar para o mundo o que eu estava fazendo para que, alguem, eventualmente, utilizasse para uso próprio.
E para ser criticado.
A parte boa destes 3 anos é que consegui resolver muitos exercícios, reencontrar velhos livros, conceitos perdidos e reaprender coisas que julgava esquecidas.
A parte ruim é que em dado momento resolvi me atentar a forma, mais que o conteudo e daí diminuí muito o ritmo.
Mas Setembro é um mês que marca muitas viradas. Os ataques de 11 de Setembro, a proclamação da Independencia do Brasil, a chegada da Primavera e por ai vai. Quem sabe, procuro em algum lugar onde ficou meu caminho perdido e retomo daí para postar coisas que podem ser uteis para alguem, além de mim.
É meio contraditorio, mas quando passei a me dar conta que era visto, me fechei.
Problemas tecnicos com meu link de internet em casa e meus equipamentos ajudaram, mas não justificam a história.
Mas nem tudo são lamentos: Me vendo no dia 11 de Setembro de 2006 e hoje, me vejo agora muito mais louco, mais confiante em pegar um exercício e resolver, mais ligado as minhas origens.
Esta semana polarizei um transistor. Há muito tempo não fazia isto e não sentia o prazer de construir um circuito tão elementar.
É bom voltar pra casa !
Abraços pra voces.
E para ser criticado.
A parte boa destes 3 anos é que consegui resolver muitos exercícios, reencontrar velhos livros, conceitos perdidos e reaprender coisas que julgava esquecidas.
A parte ruim é que em dado momento resolvi me atentar a forma, mais que o conteudo e daí diminuí muito o ritmo.
Mas Setembro é um mês que marca muitas viradas. Os ataques de 11 de Setembro, a proclamação da Independencia do Brasil, a chegada da Primavera e por ai vai. Quem sabe, procuro em algum lugar onde ficou meu caminho perdido e retomo daí para postar coisas que podem ser uteis para alguem, além de mim.
É meio contraditorio, mas quando passei a me dar conta que era visto, me fechei.
Problemas tecnicos com meu link de internet em casa e meus equipamentos ajudaram, mas não justificam a história.
Mas nem tudo são lamentos: Me vendo no dia 11 de Setembro de 2006 e hoje, me vejo agora muito mais louco, mais confiante em pegar um exercício e resolver, mais ligado as minhas origens.
Esta semana polarizei um transistor. Há muito tempo não fazia isto e não sentia o prazer de construir um circuito tão elementar.
É bom voltar pra casa !
Abraços pra voces.
Assinar:
Postagens (Atom)